Puzzles
Given three signals a, b, c, find a circuit that calculates the negations !a, !b, !c using only two inverters, but an arbitrary number of AND and OR gates.
Three bugs of different color are situated in a plane (their positions are not collinear, i.e. they do not lie on a line). They move one at a time and each bug can only move parallel to the line connecting the other two. What positions can they move to?
Transpose a rectangular, non-square matrix where rows are stored sequentially in memory in place with no extra memory (excluding of course a small number of indices to access the array). Note that there is no constraint on running time. [Doing this efficiently is a very hard problem.]
I'm not a fan of xkcd but this is a pretty good puzzle.
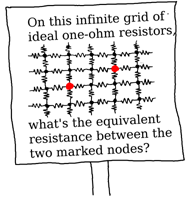
Consider a three terminal device. We will use one terminal as ground and we assume that the currents and voltages at the other two obey the following relations
V1 = Z11 I1 + Z12 I2
V2 = Z21 I1 + Z22 I2
(This is called a linear twoport). Also assume that it is passive (i.e. does not contain an energy source). If Z12 ≠ Z21, devise a way to violate the second law of thermodynamics with this device. [Note that it can be done with a deceptively simple circuit; don't think too complicated]. You might want to conclude that Z12 = Z21 always (for passive twoports), but it turns out passive devices closely resembling this can in fact be made! What have we overlooked in our previous model?
The names of 100 prisoners are placed in 100 numbered boxes. The prisoners are given time to deliberate and to come up with a group strategy and will then be placed, one by one, into the room. Each is allowed to inspect 50 boxes of their choice and has to find the box with his own name. They are not allowed to communicate with other prisoners once they have left the room. Find a strategy that lets all of them succeed 30% of the time.
Prisoners again: This time the prisoners are lined up in a queue. Each prisoner is wearing a white or a black hat. They can see the hats of the people in front of them, but not their own hat or the hats of the people behind them. They are asked one by one (starting from the back of the line) what they think the colour of their hat is. They hear the previous answers and whether they were correct or not, but may not communicate otherwise. Find a strategy that lets all but the first person succeed 100% of the time.
Three gods A, B, and C are called, in no particular order, True, False, and Random. True always speaks truly, False always speaks falsely, but whether Random speaks truly or falsely is a completely random matter. Your task is to determine the identities of A, B, and C by asking three yes-no questions; each question must be put to exactly one god. The gods understand English, but will answer all questions in their own language, in which the words for yes and no are da and ja, in some order. You do not know which word means which.